Fibonacci-Zahlen
Addiert man benachbarte Zahlen, beginnend mit 0 und 1, entsteht nachfolgende Zahlenfolge
0, 1, 1, 2, 3, 5, 8, 13, 21,….
also 0+1=1; 1+1=2; 1+2=3; 2+3=5,….
Diese scheinbar belanglose Zahlenfolge hat es aber in sich!!! Hierbei handelt es sich nämlich um die sogenannte Fibonacci-Folge bzw. um die Fibonacci-Zahlen. Benannt nach dem Mathematiker Leonardo Fibonacci.
Diese unendliche und leicht merkwürdige Zahlenfolge ist deshalb so interessant, weil sich die darin enthaltenen Zahlen sehr oft in der Natur wiederfinden.
Beispiele sind: Verteilung der Kerne bei Sonnenblumen, Blütenanordnungen bei bestimmten Blumen, Schuppenanordnungen der Ananas, u.v.a.m. Siehe auch hier..
Goldene Schnitt
Eine weitere Besonderheit ergibt sich, wenn man die benachbarten Zahlen miteinander dividiert:
Also 1:1=1; 2:1=2; 3:2=1.5; 5:3=1.67; 8:5=1.6 …………… 987:610=1.61803278
Vielleicht kann man hier schon erkennen, dass sich das Divisionsergebnis immer mehr in Richtung 1.6180339887… bewegt.
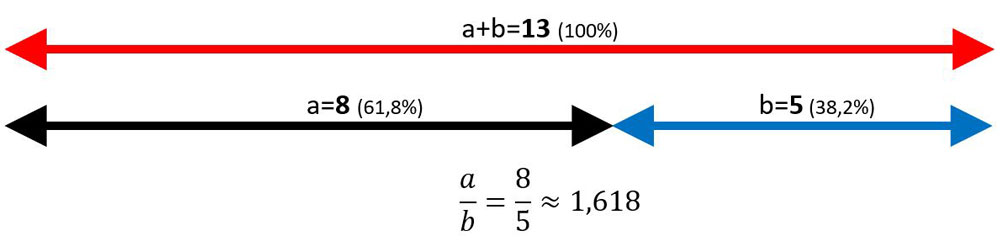
Wird nun eine Länge (Strecke) genau in diesem Verhältnis (1.618..) geteilt, spricht man von einem Goldenen Schnitt.
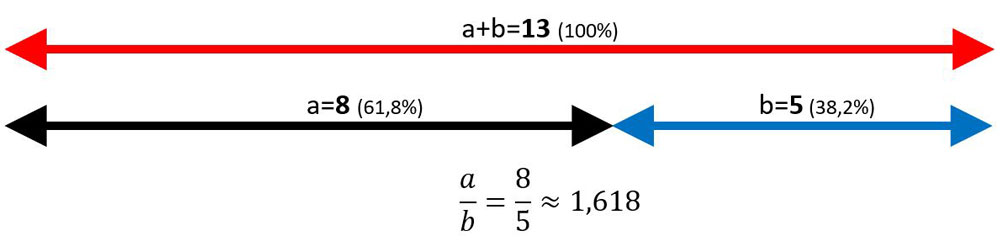
Dieses Teilungsverhältnis empfindet der Mensch als sehr angenehm und harmonisch. Auch dieses Verhältnis findet man sehr oft in der Natur. So z. B. befindet sich der Bauchnabel beim „idealen“ Menschen genau im Goldenen Schnitt. Das Verhältnis Kopflänge zu Körperlänge entspricht bei den Bienen auch dem Goldenen Schnitt. Es gibt dazu unzählige weitere Beispiele dazu in der Natur. Siehe auch hier..
So, was hat das Ganze nun mit uns Holzwerker zu tun?
Ganz einfach, es gibt uns die Möglichkeit, etwas zu konstruieren, dass am Ende vom Betrachter als „harmonisch“, „schön“ und „angenehm“ empfunden wird.
Beispiel, ich möchte einen Tisch konstruieren, wo nur die Höhe mit 90cm fix vorgegeben ist. Die Tischbreite könnte ich nun 55cm (90cm/1.62) und die Tischlänge 146cm (90cm*1.62) machen. Mit nur einer Zahl habe ich also die fehlenden Abmessungen erhalten. Mit der Hoffnung, dass die meisten Personen den Tisch nun als „gelungen“ empfinden.
Ist doch voll cool, oder? 
Auch oder gerade beim Drechseln können wir uns diese Eigenschaft zunutze machen. Um aber nicht jedesmal rechnen zu müssen, habe ich mir einen sogenannten „Goldene-Schnitt-Zirkel“ gemacht. Dieser Zirkel stellt automatisch das Teilungsverhältnis von 1.618 bzw 61,8% zu 38,2% dar.

Goldener-Schnitt-Zirkel. Damit kann das Teilungsverhältnis (goldene Schnitt) leicht übertragen werden.
Eine Anleitung von diesem Zirkel befindet sich im österreichischen Drechselforum bzw. können die Abmessungen auch leicht bei Google abgerufen werden.
Rechteckteller aus Ahorn und Pflaume
Der Start beginnt mit einem vorhandenen Ahorn-Rohling, wo die Länge mit dem Zirkel abgenommen wird. Daraus ergibt sich nun die notwendige Breite.

Die gesamte Entwicklungsgeschichte von diesem Rechteck-Teller kann hier angesehen werden: